알고리즘
[LeetCode] 78 Subsets JavaScript
sandwe
2022. 8. 8. 17:28
문제 링크
Subsets - LeetCode
Level up your coding skills and quickly land a job. This is the best place to expand your knowledge and get prepared for your next interview.
leetcode.com
문제 유형
백트래킹(Backtracking)
문제 풀이
해당 문제는 중복되지 않는 숫자들로 이루어진 배열이 주어지고, 이 숫자들로 만들 수 있는 부분집합을 배열로 반환하는 문제이다.
가능한 후보들을 모두 탐색해야 부분집합을 구할 수 있기에 가능한 후보들을 찾다가 조건을 만족하지 않으면 다시 되돌아가는 백트래킹 방식을 사용할 수 있다.
해당 문제가 재귀적으로 어떻게 동작하는지 자세히 살펴보자.
- 각 원소는 각 원소가 집합의 원소인 경우와 집합의 원소가 아닌 경우(∅)로 나뉜다. 런타임 시 backTracking 함수가 호출되고 call stack에 push된다.
재귀 종료 조건을 만족하는지 검사하고 재귀 종료 조건을 만족하지 않으면 다음 레벨을 탐색하기 위한 함수를 호출한다.
현재 0 레벨에서는 1이라는 원소가 집합의 원소인 경우와 아닌 경우로 나뉜다.
1번은 1이 집합의 원소일 때 다음 탐색을 진행하기 위한 호출이고, 2번은 1이 집합의 원소가 아닐 때 다음 탐색을 진행하기 위한 호출이다. 1번 함수가 먼저 호출되어 call stack에 push되고, 인자를 받아 함수가 실행된다.
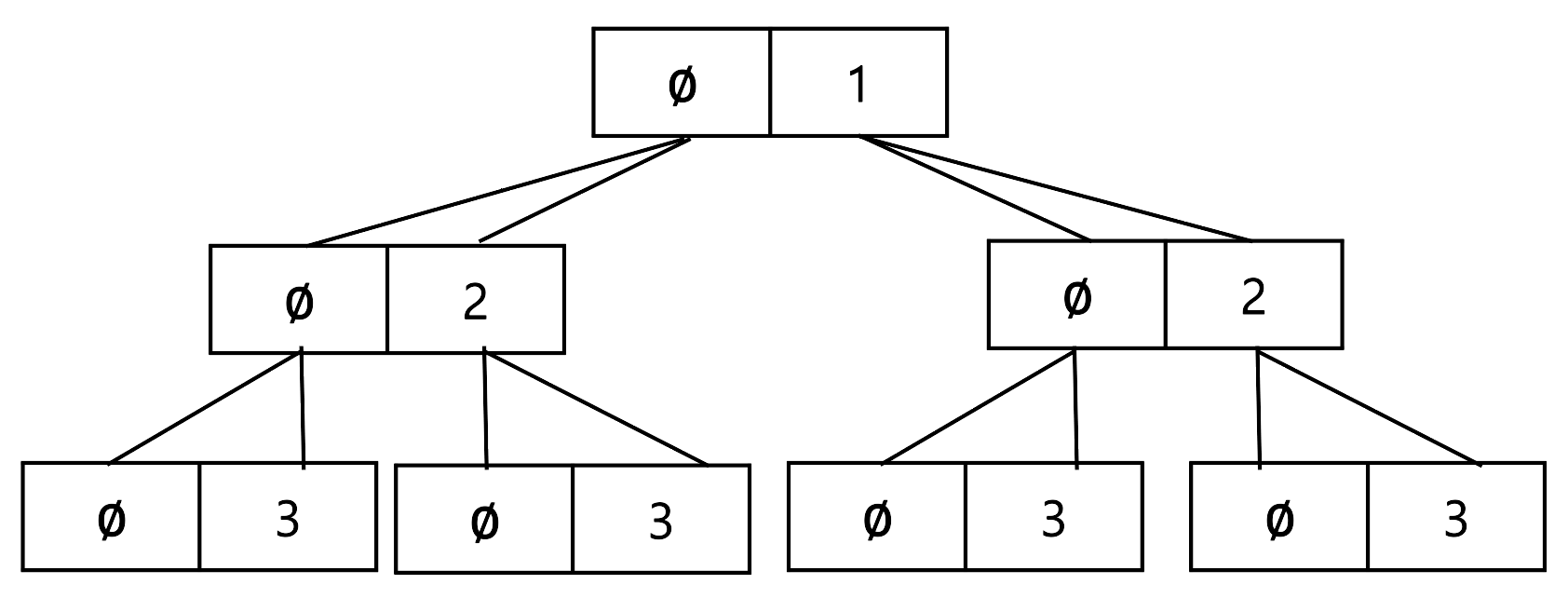

- 인자로 인덱스 1, 배열 [1]을 갖는 함수가 실행된다. 재귀 종료 조건을 만족하지 않으므로 backTracking(2, [1, 2]) 함수가 호출되고 call stack에 push된다.


- 인자로 인덱스 2, 배열 [1, 2]를 갖는 함수가 실행된다. 재귀 종료 조건을 만족하지 않으므로 backTracking(3, [1, 2, 3]) 함수가 호출되고 call stack에 push된다.

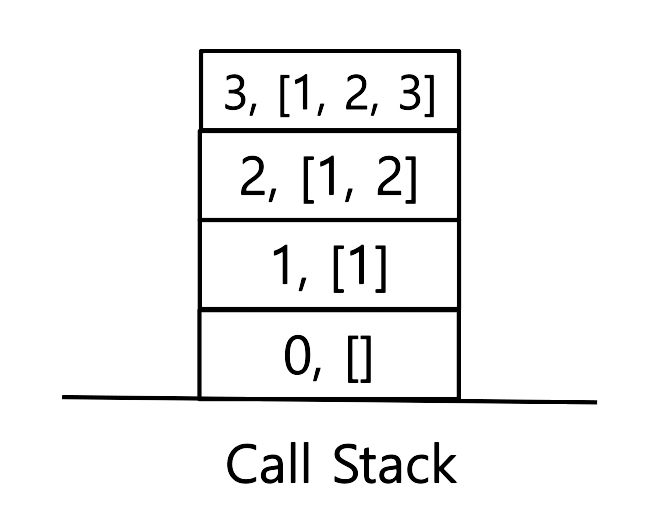
- 인자로 인덱스 3, 배열 [1, 2, 3]를 갖는 함수가 실행된다. 재귀 종료 조건을 만족하므로 결과를 담는 subsets 배열에 [1, 2, 3]을 부분집합으로 추가하고 해당 함수를 리턴해 종료한다. backTracking(3, [1, 2, 3])이 call stack에서 pop된다.

- 인자 인덱스 3, 배열 [1, 2]를 갖는 함수 2가 실행된다. 재귀 종료 조건을 만족하지 않으므로 backTracking(3, [1, 2]) 함수가 호출되고 call stack에 push된다.


- 인자로 인덱스 3, 배열 [1, 2]를 갖는 함수가 실행된다. 재귀 종료 조건을 만족하므로 결과를 담는 subsets 배열에 [1, 2]을 부분집합으로 추가하고 해당 함수를 리턴해 종료한다. backTracking(3, [1, 2])이 call stack에서 pop된다. backTracking(2, [1, 2])도 종료되어 call stack에서 pop된다. backTracking(2, [1]) 함수가 호출되고 call stack에 push된다.인자로 인덱스 2, 배열 [1]를 갖는 함수가 실행된다. 재귀 종료 조건을 만족하지 않으므로 backTracking(2, [1]) 함수가 호출되고 call stack에 push된다.

- 인자로 인덱스 2, 배열 [1]를 갖는 함수가 실행된다. 재귀 종료 조건을 만족하지 않으므로 backTracking(3, [1, 3]) 함수가 호출되고 call stack에 push된다.

- 인자로 인덱스 3, 배열 [1, 3]을 갖는 함수가 실행된다. 재귀 종료 조건을 만족하므로 결과를 담는 subsets 배열에 [1, 3]을 부분집합으로 추가하고 해당 함수를 리턴해 종료한다. backTracking(3, [1, 3])은 call stack에서 pop된다. 인자로 인덱스 3, 배열 [1]을 갖는 함수가 호출되고 call stack에 push된다.

위와 같이 가장 깊은 레벨까지 탐색해 더 이상의 레벨을 탐색할 수 없을 때 한 레벨씩 거슬러 올라와 다른 후보를 탐색하는 과정을 통해 부분집합을 구할 수 있다.
코드
const subsets = (nums) => {
const subsets = [];
const backTracking = (i, arr) => {
if (i === nums.length) {
subsets.push(arr);
return;
}
backTracking(i + 1, [...arr, nums[i]]); // 1번
backTracking(i + 1, arr); // 2번
}
backTracking(0, []);
return subsets;
};